多孔介质渗流-应力耦合模型（Biot模型）在岩土工程领域有着重要应用。岩土结构的响应是固体骨架与孔隙流体之间相互作用的结果。为了预测结构行为，常常采用有限元法对Biot方程进行数值求解。然而，当流体或固体不可压缩或接近不可压缩以及多孔介质渗透系数非常小时，方程变得病态，引起数值解的不稳定，出现孔隙流体压力紊乱的现象。要解决这个问题，所采用的单元需要满足Babuska-Brezzi条件或其等价的Zienkiewicz分片插值试验条件。遗憾的是，我们经常采用的等阶插值形式的常规有限单元（如双线性四边形Q4P4单元，图1）并不满足上述条件，无法保证计算的稳定性。为此，通常是换用位移插值函数比孔压插值函数高一阶的二次单元（即Taylor-Hood单元，如Q9P4，图1）来保证“安全”。虽然通过增加中间节点的办法增强了单元弯曲性能，同时也保证了耦合求解的稳定性，但这样带来的前处理和计算的开销却几乎成倍增加。因此，为了保证计算效率，基于低阶单元（如Q4P4单元）的多孔介质流固耦合有限元稳定化求解技术一直被研究者们所关注。    中国科学院武汉岩土力学研究所土动力学组李文涛助理研究员，长期致力于多相孔隙介质多场耦合高效数值方法的研究。基于局部投影稳定化算法，提出了多孔介质流固耦合稳定化有限元方法。该方法规避了常规混合有限元需要满足的Babuska-Brezzi条件，对等阶插值的线性单元有很好的适用性。利用合理的稳定化系数，在该方法中成功地嵌入了离散极值原理（DMP）。通过对经典的Biot固结算例的模拟分析，并与常规的Q4P4单元和Q9P4单元的计算结果进行对比，测试了稳定化的Q4P4S单元在多种情况下的性能表现。结果表明，与Q4P4单元表现出的全局震荡和Q9P4单元表现出的局部震荡不同，这里提出的稳定化单元Q4P4S具有良好的稳定性和单调性，在结构和非结构网格情况下都工作良好，计算结果与解析解得出的结果完全吻合。算例结果充分说明了该有限元稳定化求解技术能够完全消除数值求解过程中的孔隙压力震荡现象，大幅地提高了有限元方法求解Biot方程的计算精度和稳定性。    以上工作发表在期刊International Journal for Numerical Methods in Engineering上。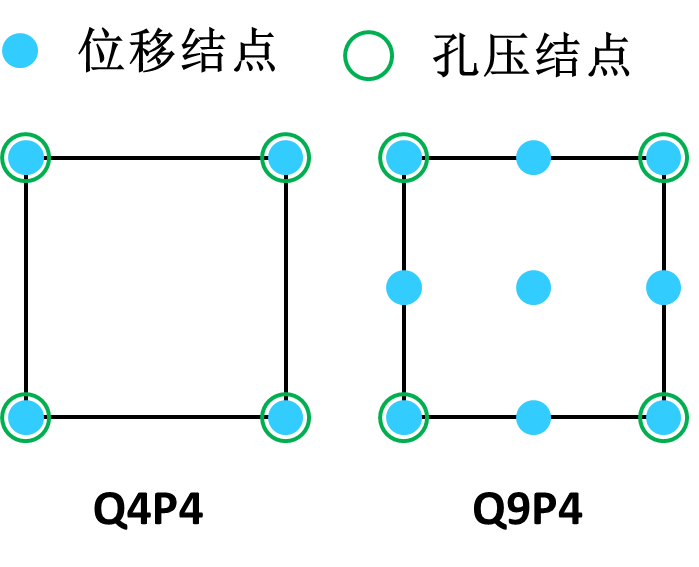   论文链接：1 图1. 不稳定的Q4P4单元和稳定的Q9P4单元 图2. Terzaghi固结算例：第一个时间步孔隙压力的竖向分布 图3. Mandel平板压缩固结算例：采用稳定的Q4P4S单元时不同时刻孔隙压力的水平分布 图4. Cylinder圆柱压缩固结问题：加载开始时孔隙压力分布图(Δt = 1s)